ニュートン-ラフソン法

目次へ

　　Newton-Raphson法

　二分法は，二つの仮定値の間に一つの解が存在する場合，確実に解を得ることができる．

近似解を得るための収束判定誤差を小さくすることで，高精度の結果を得ることができ

るが，結果を得るまでの繰返し回数が多くなる難点がある．

　そこで，もっと効率よく同等の精度の近似解を得るために考え出されたものの一つが

Newton-Raphson 法である．この方法が現在最も一般的に利用されている．ただし，

以下に述べるように，扱う方程式が微分可能であることが必要である．

１番目の近似値は次式で得られる．

　　　・・・・・・・・・・・・・・・・　（３．１）

２番目の近似値は次式で得られる．

　　　・・・・・・・・・・・・・・・・　（３．２）

同様にして，n 番目の近似値は次式で与えられる．

　　・・・・・・・・・・・・・・　（３．３）

　このように方程式が微分可能であるとき，前回で得られた近似解を用いて次の近似解

が得られる．図３．１でも分るように収束速度が二分法に比べて大きい．このことからプログ

ラミングにおいて Newton-Raphson 法が多用される．

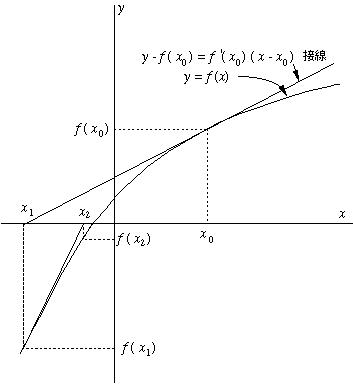
　　　　　図３．１　Newton-Raphson 法の原理

　図３．2は Newton-Raphson 法による式（２．１）の解を求めるためのフローチャー

トである。

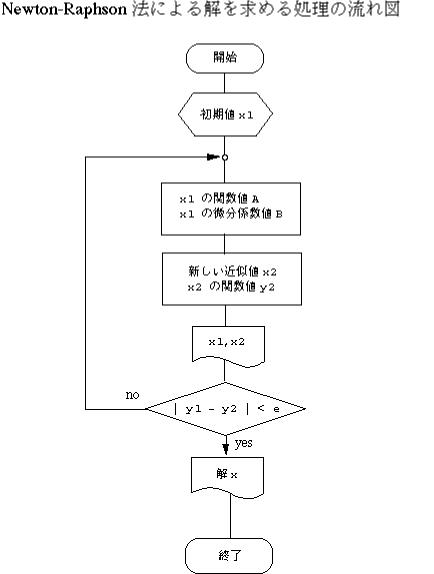
　　　　　　　　　　　　　　　　　　図３．2

　このフローチャートに従ってプログラムを記述すると、以下のようになる。　

コード　



Private Sub CommandButton1_Click()

'

' Newton - Raphson

'

    Range("A11:G111").Select

    Selection.ClearContents

    Range("A5").Select

      

      With Worksheets("Sheet1")

      X1 = .Cells(5, 1)

      E = .Cells(5, 2)

      End With

      

      i = 10:  ' 表示行の初期値

      N = 0





Retry:



1000  A = 2# * X1 - 4#

      B = X1 * X1 - 4# * X1 + 3#



      X2 = X1 - B / A

      Y2 = X2 * X2 - 4# * X2 + 3#





      i = i + 1

      N = N + 1

      With Worksheets("Sheet1")

      .Cells(i, 1) = N

      .Cells(i, 2) = X1

      .Cells(i, 3) = X2

      .Cells(i, 4) = Y2

      

      If N > 100 Then .Cells(7, 2) = "収束解が得られないので、処理を中断しました。": GoTo EndJob

      

      End With





      WRK = Abs(B - Y2)

      If WRK < E Then GoTo Result



      X1 = X2

      GoTo Retry



'     Print Out



Result:

      With Worksheets("Sheet1")

      .Cells(7, 2) = "近似解　x = " & X1

      End With



EndJob:



End Sub

サンプル