二分法

　前回の講義（2次方程式の解を求める）で示した問題では方程式の一般解が陽に

得られるので、プログラム記述も公式どおりに行えば良い。

ところが、一般には解の公式の存在する問題が沢山あるわけではなく、

むしろ直接求めることができない問題が多い。

　ある方程式が与えられているとき、その解を求める手段として近似解を得ることで

問題を解決することがよく行われる。近似解とは勿論解そのものを得ることを諦めて、

許容できる誤差を含んだ値を解として得るものである。

　ここでは、方程式（２．１）の解を二分法によって近似解で得る方法を述べる。

方程式の解はは解の公式から実数 1 と 3 であることは明らかであるが、それに依ら

ない方法として示す。

　図２．１は方程式の左辺を関数として描かれるグラフである。グラフが x 軸と交

わる値が 1 と 3 であるのは、方程式の解であることは明らかである。

　　　・・・・・・・・・・・・・・・　（２．１）

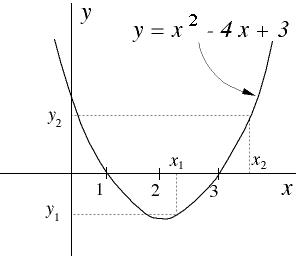
　　　　　　　図２．１　方程式のグラフ

　今、図２．２のように解の一方付近のグラフに注目してみると、解を挟む２つ

の仮定値 x1 および x2 を与え、それらの関数値 y1 および y2 が互いに異符号で

あるとき、真の解は x1 と x2 の間に存在することが分る。このように関数が x 軸

と交わるとき、それを挟む２つの関数値は互いに異符号である。このことを利用し

て解を挟む２つの x 値の間隔を逐次狭めていくことで近似値の精度を上げていく。

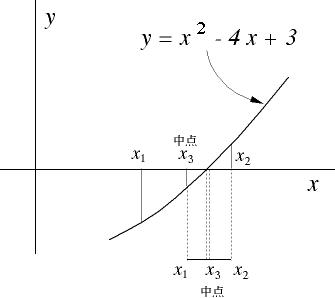
　　　　　　　　　図２．２　二分法の原理

　今、 x1 と x2 の中点 x3 をとり、その関数値を y3 とすれば、中点の関数値の

符号を調べれば、二分した区間のどちらの方に解が存在するかが分る。すはわち、

「両側の一方の関数値と中間値の関数値が異符号である区間に解が存在する。」と

いう原理を利用すると、図２．２に示されるように、改めて解を含む区間の両 x 座

標をx1 と x2 と更新して、以下上記の手順を繰返して、所定の精度が得られたら、

結果を出力すれば良い。こういった繰返し演算を収斂（しゅうれん）計算と呼ぶ。

　図２．３は二文法による式（２．１）の解を求めるためのフローチャートである。

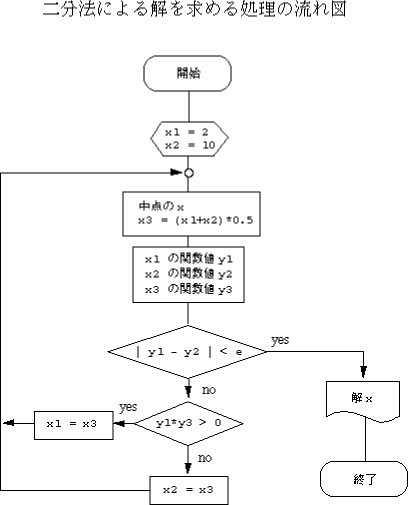
　　　　　　　　　　　　　　図２．３

　このフローチャートに従ってプログラムを記述すると、以下のようになる。　

コード　

Function F(X)
          F = X * X - 4# * X + 3#
End Function


Private Sub CommandButton1_Click()
'     Bisection Method
'

    Range("A11:G111").Select
    Selection.ClearContents
    Range("A5").Select
      
      With Worksheets("Sheet1")
      X1 = .Cells(5, 1)
      X2 = .Cells(5, 2)
      E = .Cells(5, 3)
      End With
      
      i = 10:  ' 表示行の初期値
      N = 0
'
Retry:
'
      X3 = (X1 + X2) * 0.5

      Y1 = F(X1)
      Y2 = F(X2)
      Y3 = F(X3)

      i = i + 1
      N = N + 1
      With Worksheets("Sheet1")
      .Cells(i, 1) = N
      .Cells(i, 2) = X1
      .Cells(i, 3) = X2
      .Cells(i, 4) = X3
      
      .Cells(i, 5) = Y1
      .Cells(i, 6) = Y2
      .Cells(i, 7) = Y3
      
      If N > 100 Then .Cells(7, 2) = "収束解が得られないので、処理を中断しました。": GoTo EndJob
      End With

      If Abs(Y1) < E Then GoTo Result1
      If Abs(Y2) < E Then GoTo Result2
      If Abs(Y3) < E Then GoTo Result3
      
      PRDCT = Y1 * Y3
      
      If PRDCT > 0# Then
           X1 = X3
      Else
      If PRDCT < 0# Then
           X2 = X3
      End If
      End If
      
      GoTo Retry

Result1:

      With Worksheets("Sheet1")
      .Cells(7, 2) = "近似解　x = " & X1
      End With
GoTo EndJob

Result2:

      With Worksheets("Sheet1")
      .Cells(7, 2) = "近似解　x = " & X2
      End With
GoTo EndJob
      
Result3:

      With Worksheets("Sheet1")
      .Cells(7, 2) = "近似解　x = " & X3
      End With
EndJob:

End Sub
	

サンプル